亲爱的数学迷们，今天咱们来聊聊一个既神秘又熟悉的数学小精灵——幂函数！它可是数学世界里的小魔术师，能将简单的数字变成神奇的幂次方。准备好了吗？让我们一起揭开幂函数的神秘面纱，探索它的奇妙世界吧！

一、幂函数的诞生

想象你手中有一堆苹果，你想知道如果每个苹果都翻倍，你会得到多少苹果呢？这时候，幂函数就登场了。它就像一个魔法公式，能帮你轻松计算出结果。在数学的世界里，幂函数的形式是这样的：\\( f(x) = x^n \\)，其中 \\( x \\) 是底数，\\( n \\) 是指数。

二、幂函数的魔力

1. 指数的奥秘：指数就像一个放大镜，它能将底数放大或缩小。比如，\\( 2^3 \\) 就是将 2 放大 3 倍，结果是 8。而 \\( 2^{-3} \\) 则是将 2 缩小 3 倍，结果是 \\( \\frac{1}{8} \\)。

2. 负指数的魔法：负指数就像一个反向的放大镜，它将底数变成倒数。比如，\\( 2^{-2} \\) 就是将 2 变成 \\( \\frac{1}{2^2} \\)，结果是 \\( \\frac{1}{4} \\)。

3. 零指数的神奇：零指数就像一个魔法门，它将任何非零数变成 1。比如，\\( 2^0 \\) 就是将 2 变成 \\( \\frac{1}{2^0} \\)，结果是 1。

三、幂函数的应用

1. 物理世界：在物理学中，自由落体运动的高度公式 \\( h = \\frac{1}{2}gt^2 \\) 就涉及了幂函数。这里，\\( g \\) 是重力加速度，\\( t \\) 是时间。

2. 工程领域：在工程设计中，幂函数常用于计算材料强度、结构稳定性等。

3. 经济领域：在经济学中，幂函数用于描述经济增长、人口增长等。

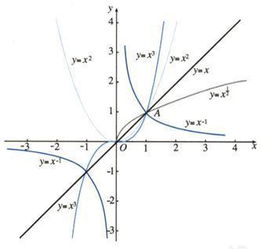
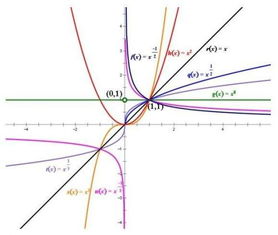
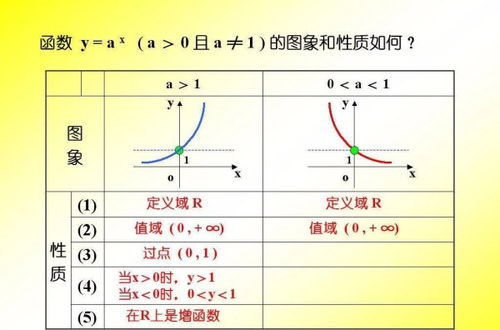
四、幂函数的图像

幂函数的图像就像一条蜿蜒的曲线，它随着指数的变化而变化。当指数为正数时，图像呈上升趋势；当指数为负数时，图像呈下降趋势。

五、幂函数的运算

1. 乘法规则：当两个同底数的幂相乘时，指数相加。比如，\\( 2^3 \\times 2^2 = 2^{3 2} = 2^5 \\)。

2. 除法规则：当两个同底数的幂相除时，指数相减。比如，\\( 2^5 \\div 2^2 = 2^{5-2} = 2^3 \\)。

3. 幂的乘方：当一个幂的指数再次乘方时，指数相乘。比如，\\( (2^3)^2 = 2^{3 \\times 2} = 2^6 \\)。

4. 负指数：负指数表示倒数关系。比如，\\( 2^{-2} = \\frac{1}{2^2} = \\frac{1}{4} \\)。

5. 零指数：任何非零数的零次幂等于 1。比如，\\( 2^0 = 1 \\)。

6. 分数指数：分数指数表示开方与幂的结合。比如，\\( 2^{\\frac{1}{2}} = \\sqrt{2} \\)。

在这个充满魔力的数学世界里，幂函数就像一位神奇的魔术师，它能将简单的数字变成神奇的幂次方。让我们一起探索这个奇妙的世界，感受数学的魅力吧！